Modern RL algorithms typically resort to function approximation (e.g., deep neural networks) when faced with large state and action spaces. However, these approximations come with significant trade-offs: they often incur optimization difficulties, limited theoretical guarantees, and substantial computational costs. This raises a natural question:
In this survey, we provide an answer to this question through the lens of spectral representations.
Inspired by linear MDPs, we consider a more generalized factorization. For any well-behaved transition operator $\mathbb{P}$ and reward function $r$, there exist two feature maps $\boldsymbol{\phi}: \mathcal{S}\times\mathcal{A}\to \mathcal{H}$, $\boldsymbol{\mu}:\mathcal{S}\to\mathcal{H}$ and a vector $\boldsymbol{\theta}_r\in\mathcal{H}$ for some proper Hilbert space $\mathcal{H}$, such that $$ \begin{aligned} \mathbb{P}(s'|s, a) &=\langle\boldsymbol{\phi}(s, a), \boldsymbol{\mu}(s')\rangle_{\mathcal{H}},\\ r(s, a)&=\langle \boldsymbol{\phi}(s, a), \boldsymbol{\theta}_r\rangle_{\mathcal{H}}.\\ \end{aligned} $$ In fact, such decomposition always exists. The factorization instantly leads to the linearity of $Q$-value functions: $$ \begin{aligned} Q^\pi(s, a) &= r(s, a)+\gamma \int_{\mathcal{S}} \mathbb{P}(s'|s, a)V(s')\mathrm{d}s'\\ &=\langle \boldsymbol{\phi}(s, a), \boldsymbol{\theta}_r\rangle_{\mathcal{H}}+\gamma \langle \boldsymbol{\phi}(s, a), \int_{\mathcal{S}} \boldsymbol{\mu}(s')V(s')\mathrm{d}s' \rangle_{\mathcal{H}}\\ &=\bigg\langle\boldsymbol{\phi}(s, a),\underbrace{\boldsymbol{\theta}_r+\gamma \int_{\mathcal{S}} \boldsymbol{\mu}(s')V(s')\mathrm{d}s'}_{\boldsymbol{\eta}^\pi}\bigg\rangle_{\mathcal{H}} \end{aligned} $$ i.e., $Q$-value functions lie in the linear function space spanned by the same feature map $\boldsymbol{\phi}(s, a)$. This implies that:
✔ Theoretically, we can reduce the complexity by only considering linear $Q$-value functions;
✔ Practically, $\boldsymbol{\phi}(s, a)$ can serve as a effective representation for $Q$-value functions;
✔ Intuitively, $\boldsymbol{\phi}(s, a)$ encodes the essential information of the system dynamics.
Given its significance, we build a systematic framework for utilizing $\boldsymbol{\phi}(s, a)$ for RL. We term $\boldsymbol{\phi}(s, a)$ as the spectral representations.In this case, there exists $\boldsymbol{\phi}: \mathcal{S}\times\mathcal{A}\to \mathbb{R}^d$ and $\boldsymbol{\mu}:\mathcal{S}\to\mathbb{R}^d$ such that: $$ \begin{aligned} \mathbb{P}_{\text{Linear}}(s'|s, a) &=\boldsymbol{\varphi}(s, a)^\top\boldsymbol{\nu}(s'), \end{aligned} $$ and the spectral representation is $$ \boldsymbol{\phi}_{\text{Linear}}(s, a) = \boldsymbol{\varphi}(s, a). $$
○ Equivalent to linear MDPs
✗ The linear assumption hurts the expressiveness.
The latent variable is $z\in\mathcal{Z}$ and there exist two probability measures $\varphi(z|s, a)$ and $\nu(s'|z)$ such that: $$ \begin{aligned} \mathbb{P}_{\text{LV}}(s'|s, a) &=\int_{\mathcal{Z}} \varphi(z|s, a)\nu(s'|z)\mathrm{d}z. \end{aligned} $$ In this case, the spectral representation is $$ \boldsymbol{\phi}_{\text{LV}}(s, a) = [\varphi(z_1|s, a), \varphi(z_2|s, a), \ldots]^\top\quad \text{ for } z_i\in \mathcal{Z}. $$
○ Infinite-dimensional but can be approximated by Monte-Carlo sampling;
✔ More expressive the the linear case.
Energy-based models (EBMs) associate the transition probability with an energy function $E(s, a, s')$: $$ \begin{aligned} \mathbb{P}_{\text{EBM}}(s'|s, a)&=\frac{\exp(E(s, a, s'))}{Z(s, a)}=\frac{\exp(\boldsymbol{\varphi}(s, a)^\top\boldsymbol{\nu}(s'))}{Z(s, a)}, \end{aligned} $$ Through random Fourier features, we can construct $$ \boldsymbol{\phi}_{\text{EBM}}(s, a) = \frac{\exp(\|\boldsymbol{\varphi}(s, a)\|^2)}{Z(s, a)}\boldsymbol{\zeta}_N(\boldsymbol{\varphi}(s, a)), $$ where $\boldsymbol{\zeta}_N(\boldsymbol{\varphi}(s, a))$ is the random Fourier feature of $\boldsymbol{\varphi}(s, a)$.
✔ Most flexible in terms of expressiveness.
Direct maximum likelihood estimation is intractable ... $$ \begin{aligned} &\max_{\boldsymbol{\phi}, \boldsymbol{\mu}} \ \mathbb{E}_{(\mathbf{s}, \mathbf{a}, \mathbf{s}') \sim \mathcal{D}}\left[\log \langle\boldsymbol{\phi}(s, a), \boldsymbol{\mu}(s')\rangle\right]\\ \end{aligned} $$ $$ \ \ \ \text{s.t.}\ \forall(s, a), \ \ \int_\mathcal{S} \langle\boldsymbol{\phi}(s, a), \boldsymbol{\mu}(s')\rangle\mathrm{d}s'=1, $$ But fortunately tractable alternatives exist for different formulations.
Since our theory suggests that spectral representations can represent $Q$-value functions sufficiently, we build our $Q$-value functions as $Q_{\theta, \xi}(s, a)=Q_{\xi}(\boldsymbol{\phi}_\theta(s, a))$, where the specific form depends on the choice of spectral representations. This allows spectral representations to be seamlessly integrated into any reinforcement learning (RL) pipeline. Meanwhile, each of the learning methods described in the previous section naturally realizes an effective RL algorithm.
Extension to POMDPs: Assuming the POMDPs satisfy the $L$-decodability condition, which implies that the $L$-step history $x_t=(o_{t-L+1}, a_{t-L+1}, \ldots, o_t)$ is a sufficient statistic for the current system state, we can derive spectral representations for POMDPs using the $L$-step decomposition: $$ \begin{aligned} \mathbb{P}^\pi_L(x_{t+L}|x_t, a_t) &= \langle\boldsymbol{\varphi}(x_t, a_t), \boldsymbol{\nu}^{\tilde{\pi}}(x_{t+L})\rangle_{\mathcal{H}},\\ r^\pi_L(x_t, a_t)&=\sum_{i=0}^{L-1}\gamma^ir_{t+i}=\langle\boldsymbol{\varphi}(x_t, a_t), \boldsymbol{\theta}_r^{\tilde{\pi}}\rangle_{\mathcal{H}},\\ \end{aligned} $$ The $L$-step Bellman equation then leads to $Q^\pi(x_t, a_t)=\langle\boldsymbol{\varphi}(x_t, a_t), \boldsymbol{\theta}_r^{\tilde{\pi}}+\gamma^L\boldsymbol{\nu}^{\tilde{\pi}}(x_{t+L})\rangle_{\mathcal{H}}$, making $\boldsymbol{\varphi}(x_t, a_t)$ the spectral representation that can sufficiently express the $Q$-value function.
We consider the following instantiations of spectral representation-based RL algorithms:
Speder |
1. Linear Formulation + Ⅰ. Spectral Contrastive Learning |
LV-Rep |
2. Latent Variable Formulation + Ⅱ. Variational Learning |
Diff-SR |
3. Energy-Based Formulation + Ⅲ. Score Matching |
CTRL-SR |
3. Energy-Based Formulation + Ⅳ. Noise Contrastive Learning |
TD3 Algorithm.
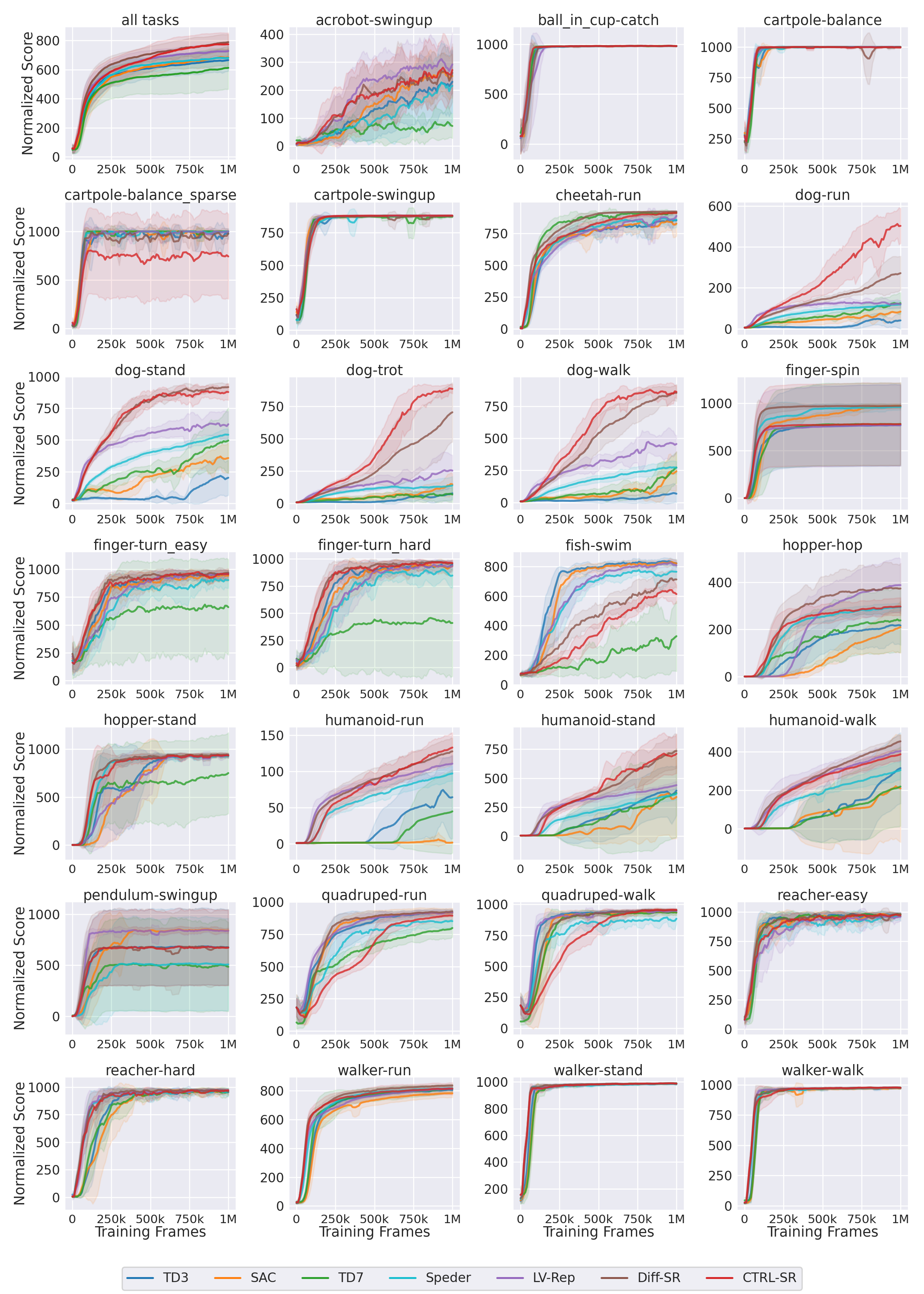
dog-* and humanoid-* tasks.
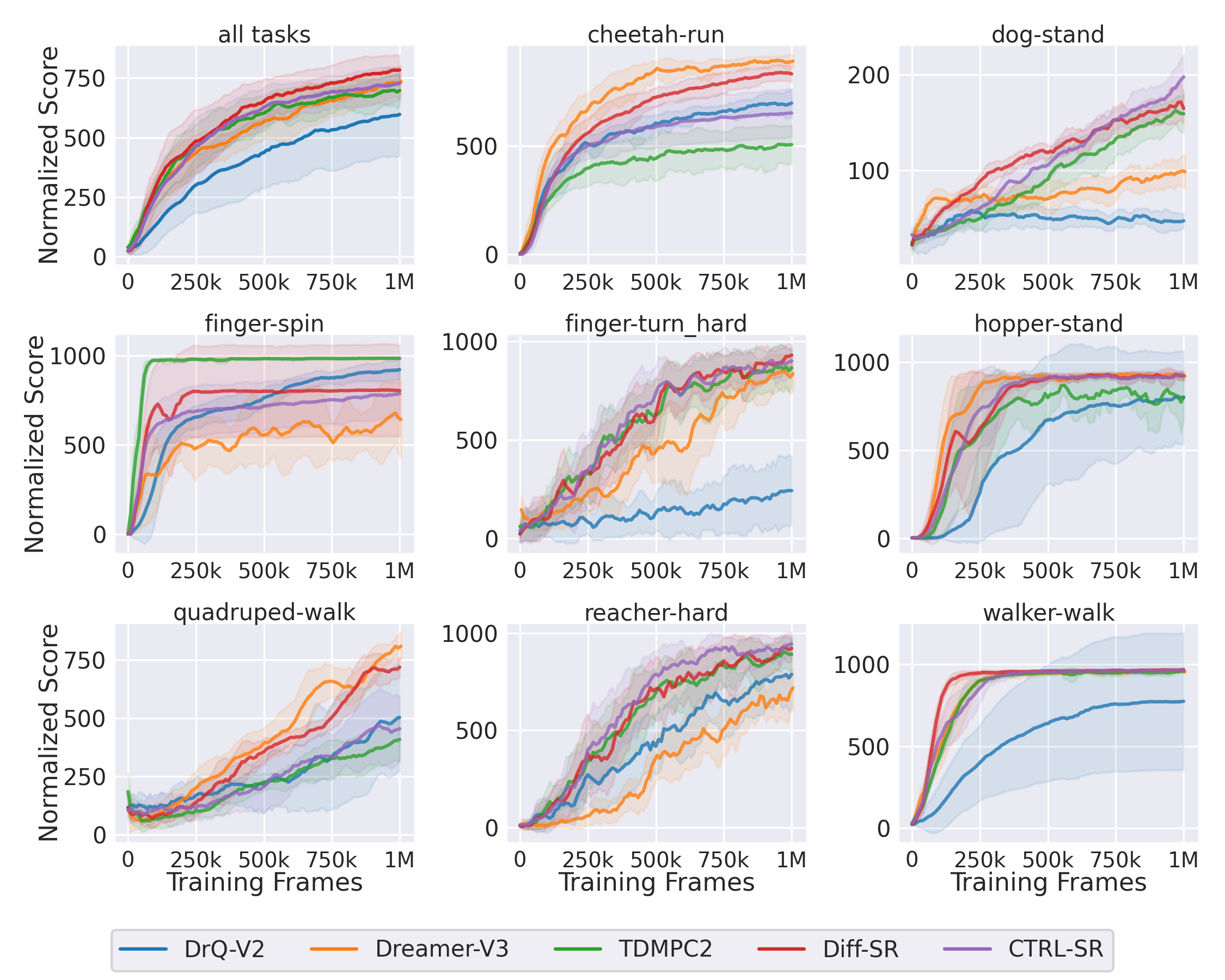
Diff-SR and CTRL-SR require significantly less training time than model-based competitors, since the representation-based methods avoid the costly model-based planning procedure.
@inproceedings{ren2023latent,
title={Latent Variable Representation for Reinforcement Learning},
author={Ren, Tongzheng and Xiao, Chenjun and Zhang, Tianjun and Li, Na and Wang, Zhaoran and Schuurmans, Dale and Dai, Bo},
booktitle={International Conference on Learning Representations (ICLR)},
year={2023}
}
@inproceedings{zhang2022making,
title={Making linear mdps practical via contrastive representation learning},
author={Zhang, Tianjun and Ren, Tongzheng and Yang, Mengjiao and Gonzalez, Joseph and Schuurmans, Dale and Dai, Bo},
booktitle={International Conference on Machine Learning (ICML)},
pages={26447--26466},
year={2022},
}
@inproceedings{zhang2024provable,
title={Provable Representation with Efficient Planning for Partially Observable Reinforcement Learning},
author={Zhang, Hongming and Ren, Tongzheng and Xiao, Chenjun and Schuurmans, Dale and Dai, Bo},
booktitle={International Conference on Machine Learning (ICML)},
pages={59759--59782},
year={2024},
}
@inproceedings{ren2023spectral,
title={Spectral Decomposition Representation for Reinforcement Learning},
author={Ren, Tongzheng and Zhang, Tianjun and Lee, Lisa and Gonzalez, Joseph E and Schuurmans, Dale and Dai, Bo},
booktitle={International Conference on Learning Representations (ICLR)},
year={2023}
}
@article{shribak2024diffusion,
title={Diffusion Spectral Representation for Reinforcement Learning},
author={Shribak, Dmitry and Gao, Chen-Xiao and Li, Yitong and Xiao, Chenjun and Dai, Bo},
journal={Annual Conference on Neural Information Processing Systems (NeurIPS)},
year={2024}
}